
【統計学入門】記述統計・推測統計とは?|データ活用戦略講座②
2023.11.28
前回の記事では、データの集め方・活用方法について事例を交えながらご紹介しました。
今回は「データの見方・分析方法」の観点から、統計の基礎知識である「記述統計」と「推測統計」について解説します。
この記事を最後まで読むことで、統計学の基礎知識をはじめ、データ分析・データ活用の方法と注意点について理解を深めることができるでしょう。
記述統計とは
記述統計とは
皆さんは「記述統計」という言葉を耳にしたことはありますか。
「記述統計」とは、与えられたデータの性質を明らかにする統計学の分野のことです。
データの示す傾向や性質を把握する際に使用します。
例えば、平均値や中央値などの代表値をはじめ、データをグラフで可視化するなど、データの特徴を理解しやすくする手法が挙げられます。
記述統計の重要性
なぜ、「記述統計」がデータ分析の際に重要なのでしょうか。
それは、「データ」があるだけではデータの特徴や傾向を掴めず、データを上手く活用できないからです。
例えば、あなたが自社X製品の日本国内における実態を把握したいとします。
そこで、以下の項目についてデータを収集するため、web調査を実施しました。
〇収集したいデータ
1.自社X製品の日本国内における認知率
2.認知者における製品利用率
3.製品利用者におけるX製品への満足度
4.X製品不満者における不満点
5.製品利用者における改良版Z製品の購入意向率
〇web調査の概要
・対象エリア:47都道府県
・対象年齢:20歳~69歳
・割付:男女×20代/30代/40代/50代/60代
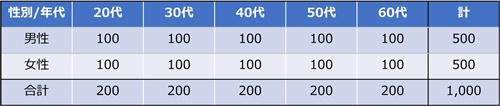
計10セル 各セル100名
・回答者数:計1,000名
表1.性年代別割付
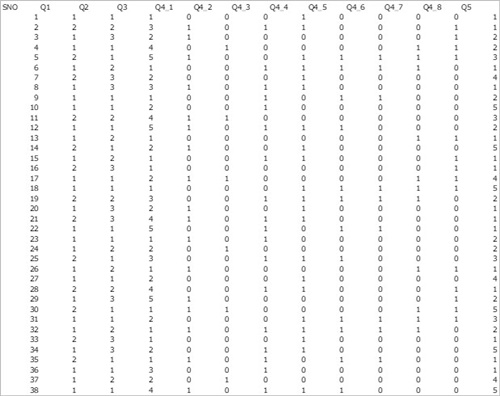
ところが、アンケート終了後に回収したExcelデータは以下のような形でした。
図1.回収データ
これでは、X製品の認知率や製品利用率などの実態を簡単に把握することができません。
そこで、「記述統計」を用いデータを理解しやすい形に変換することで、データの特徴や傾向を掴むことができます。
記述統計の限界とその解決策
「記述統計」はデータを理解やすい形に変換することで、与えられたデータの特徴や傾向を掴むことができると解説してきました。では、日本人全体の傾向が知りたい場合はどうでしょうか。日本人全員のデータを取得するのは、コスト面から見ても現実的な方法とは言えませんよね。
一方で、日本人1000名のデータを集めて分析するなら現実的かと思います。
さらに、この1000名のデータで日本人全体の特徴が推測できれば、コストを抑えながら、現実に即した市場実態を把握できますよね。
そこで登場するのが、次章で紹介する「推測統計」という考え方です。
推測統計とは
推測統計とは
「推測統計」とは、標本から母集団の特徴、性質を推定する統計学の分野のことです。
母集団、すべてのデータを調査するのが難しい場合に用いられます。
母集団と標本
「母集団」と「標本」の意味と関係性は以下の通りです。
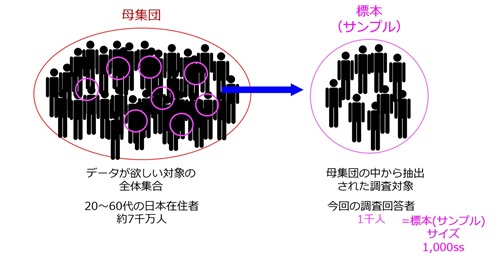
図2.母集団と標本の関係性
「母集団」が推測したい全体集合であるのに対し、「標本」は母集団の中から抽出した調査対象を指します。上図の場合、20~60代の日本在住者約7000万人が「母集団」、調査対象者1000人が「標本」です。
標本を抽出する際の注意点
標本を抽出する際に注意すべきなのが、抽出はランダムに行うという点です。(無作為抽出・ランダムサンプリング)
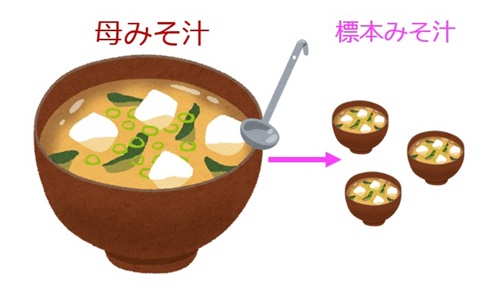
例えば、以下のように、大きな鍋のみそ汁(母みそ汁)の味を確かめたいとします。
図3.母集団から標本を抽出する際のイメージ
あなたは、母みそ汁をかき混ぜず、みそ汁の具材を多めに取ったり、鍋の上部の母みそ汁だけをよそい味を確かめた結果、味も具材の量もバラバラでした。この場合、母みそ汁の本来の味が分かったと言えるでしょうか。もちろん、言えませんよね。
母みそ汁の味をより正確に確かめるには、母みそ汁をよくかき混ぜた上で、小さな器によそう必要があります。
実際に母集団を推測する際も同様で、データに偏りのある標本は母集団を代表しているとは言えません。
そのため、標本を母集団の縮図(代表)とする為には、サンプルをランダム(無作為)に抽出する事が大切です。
母集団と標本のズレ
前節で、母集団から標本を抽出する際は標本をランダムに抽出し、標本の数値をできる限り母集団の縮図(代表)とする必要があるとお伝えしました。
しかし実際には、母集団と標本の値には必ず差が生じます。その差のことを「標準誤差」と言います。標準誤差は、標本のサンプルサイズの大きさによって変動し、その関係を整理した表が下記の「標準誤差早見表」です。
図4. 標準誤差早見表(95%信頼区間)
例えば、サンプルサイズが400で、サービスの認知率が30%であったと仮定しましょう。
下記のように、「サンプルサイズ400」の列と「スコア30%」の行が交差する値が「4.6」とあるため、標本誤差は±4.6%と読み取れます。
図5.標準誤差早見表(95%信頼区間)の見方
つまり、アンケート調査で出た「認知率30%」という結果は±4.6%(25.4%~34.6%)の範囲に母集団の認知率(本当の認知率)があることが分かります。
なお、標本のサンプルサイズを大きくすると標準誤差は小さくなりますが、調査費用もその分かかるため、調査結果の精度と予算との折り合いをつけることが大切です。
まとめ
今回は「データの見方・分析方法」の観点から、統計の基礎知識である「記述統計」と「推測統計」について解説しました。以下、今回のまとめです。
〇記述統計
・記述統計とは、与えられたデータの性質を明らかにする統計学の分野のこと。
・データを要約・分析することで、データの特徴や傾向を掴むことができる。
〇推測統計
・標本から母集団の特徴、性質を推定する統計学の分野のこと。
・母集団のすべてのデータを調査するのが難しい場合に用いられる。
・標本は必ず無作為(ランダム)に抽出する必要がある。
・標本と母集団の値には必ず差(標準誤差)が生じるので、どの範囲に母数の値(本当の値)があるのか「標準誤差早見表」で確認する。
この記事を通して、統計学の基礎知識をはじめ、データ分析・データ活用の方法と注意点について理解を深めて頂ければ幸いです。
DataLab株式会社では、データ活用の課題全般に関してご支援いたします。お気軽にお問い合わせくださいませ。

big.jpg)
の見方big.jpg)